Interpreter Pattern

인터프리터 패턴 (Interpreter Pattern)

자주 등장하는 문제를 간단한 언어로 재정의하고 재사용하는 패턴이다.

반복되는 문제 패턴을 언어나 문버으로 재정의하고 확장할 수 있다.

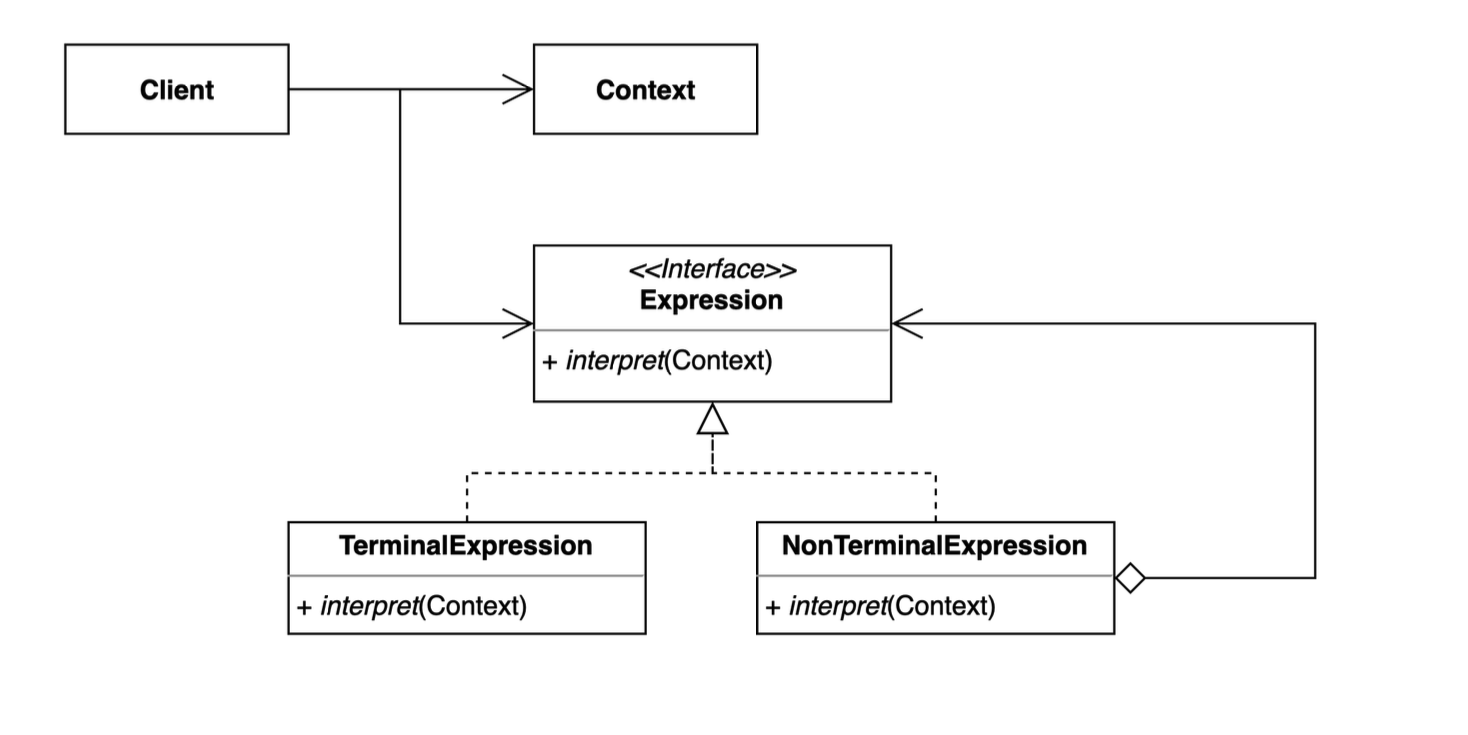
패턴 구조

1. Context: 모든 expression에서 사용하는 공통된 정보를 가진 클래스
2. AbstractExpression: 인터프리터에서 사용하는 인터페이스를 정의하는 클래스
3. TerminalExpression: 한번 해석하고 종료되는 Expression
4. NonterminalExpression: 종료되지 않고 다른 Expression을 호출하는 Expression. 그 다른 Expression TerminalExpression일수 있고 NonterminalExpression일 수 있다.

패턴 적용 전

Postfix Notation을 계산하는 프로그램을 만들어보자.

Postfix Notation은 연산자가 피연산자 뒤에 나오는 표기법이다. 예를 들어 3 + 4는 3 4 +로 표현된다. 만약 123+-라면 1 - (2 + 3)으로 계산된다.

이를 계산하는 코드는 다음과 같다.

class PostfixNotation(val expression: String) {
  
  fun calculate(): Int {
    val stack = Stack<Int>()
    val tokens = expression.split(" ")
    
    for (token in tokens) {
      if (token == "+") {
        val right = stack.pop()
        val left = stack.pop()
        stack.push(left + right)
      } else if (token == "-") {
        val right = stack.pop()
        val left = stack.pop()
        stack.push(left - right)
      } else {
        stack.push(token.toInt())
      }
    }
    return stack.pop()
  }
}

이 때 새로운 연산자나 표현식을 추가하고 싶다면 다음과 같이 코드를 계속해서 수정해야 한다.

class PostfixNotation(val expression: String) {
  
  fun calculate(): Int {
    val stack = Stack<Int>()
    val tokens = expression.split(" ")
    
    for (token in tokens) {
      if (token == "+") {
        val right = stack.pop()
        val left = stack.pop()
        stack.push(left + right)
      } else if (token == "-") {
        val right = stack.pop()
        val left = stack.pop()
        stack.push(left - right)
      } else if (token == "*") {
        val right = stack.pop()
        val left = stack.pop()
        stack.push(left * right)
      } else if (token == "/") {
        val right = stack.pop()
        val left = stack.pop()
        stack.push(left / right)
      } else {
        stack.push(token.toInt())
      }
    }
    return stack.pop()
  }
}

패턴 적용 후

이러한 문제를 해결하기 위해 인터프리터 패턴을 적용해보자.

// AbstractExpression
interface PostfixExpression {
  fun interpret(context :Map<Char, Int>): Int
}

// TerminalExpression 
// 단순히 숫자를 반환하고 끝나는 표현
class NumberExpression(val char: Char) : PostfixExpression {
  override fun interpret(context :Map<Char, Int>): Int {
    return context[char]
  }
}

// 더하기 표현 NonterminalExpression 
// 두 표현식에서 interpret 메서드를 호출하고 더한 값을 반환
class AddExpression(val left: PostfixExpression, val right: PostfixExpression) : PostfixExpression {
  override fun interpret(context :Map<Char, Int>): Int {
    return left.interpret(context) + right.interpret(context)
  }
}

// 빼기 표현 NonterminalExpression
// 두 표현식에서 interpret 메서드를 호출하고 뺀 값을 반환
class SubtractExpression(val left: PostfixExpression, val right: PostfixExpression) : PostfixExpression {
  override fun interpret(context :Map<Char, Int>): Int {
    return left.interpret(context) - right.interpret(context)
  }
}

이 후 PostfixParser라는 유틸 클래스를 만들어 PostfixNotation을 해석하고 계산하는 코드를 작성한다.

class PostfixParser {
  companion object {
    fun parse(expression: String): PostfixExpression {
      val stack: Stack<PostfixExpression> = Stack<PostfixExpression>()
      for (c in expression.toCharArray()) {
        stack.push(getExpression(c, stack))
      }
      return stack.pop()
    }

    fun getExpression(c: Char, stack: Stack<PostfixExpression>): PostfixExpression {
      return when (c) {
        '+' -> AddExpression(stack.pop(), stack.pop())
        '-' -> {
          val right = stack.pop()
          val left = stack.pop()
          SubtractExpression(left, right)
        }
        else -> NumberExpression(c)
      }
    }

  }
}

이제 실제로 xyz+-a+를 계산하는 코드는 다음과 같다.

import java.util.Map

fun main() {
  val expression: PostfixExpression = PostfixParser.parse("xyz+-a+")
  val result: Int = expression.interpret(Map.of('x', 1, 'y', 2, 'z', 3, 'a', 4))
  println(result) // 0
}

중요한 점은 저번 Composit 패턴과 같이 트리 구조를 사용한다는 것이다.

먼저 스택에 있는 Expression은 xyza처럼 숫자가 아닌 문자로 이루어진 표현식이다. 이 후 실제 interpret 메서드를 호출할 때는 Map을 인자로 받아서 해당 문자에 해당하는 값을 반환한다.

1. x y z가 각각 스택에 NumberExpression으로 들어간다. => [Number(x), Number(y), Number(z)]
2. • 연산자는 z와 y를 더한 값을 반환하는 AddExpression으로 변환한다. => [Number(x), ADD(Number(z), Number(y))] [1, 5]
3. • 연산자는 AddExpression과 x를 뺀 값을 반환하는 SubtractExpression으로 변환한다. => [Sub(Number(x), ADD(Number(y)), Number(z))] 1 -5 = -4
4. a가 NumberExpression으로 변환되고 Stack에 추가된다. => [위 3에 해당하는 Sub, Number(a)] [-4, 4]
5. • 연산자는 SubtractExpression과 a를 더한 값을 반환하는 AddExpression으로 변환한다. => [Add(위 3에 해당하는 Sub, Number(a)] -4 + 4 = 0
6. 최종적으로 AddExpression의 interpret 메서드를 호출하면 위 5에서 만든 AddExpression이 호출되고 그 결과를 반환한다. => 0

(Numebr: NumberExpression, Add: AddExpression, Sub: SubtractExpression)

장단점

장점

• 자주 등장하는 문제 패턴을 문법으로 정의해 재사용성이 높아진다.
• 기존 코드를 변경하지 않고 새로운 Expression을 추가할 수 있다.

단점

• 복잡한 문법을 표현하려면 Expression과 Parser가 복잡해진다.

Reference

• 코딩으로 학습하는 GoF의 디자인 패턴 - 백기선